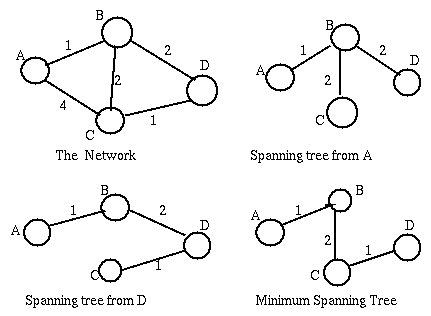
[Stable Properties and Self-Stabilizing Systems], [Two Distributed Spanning Tree Algorithms], [Dijkstra's Shortest Path Algorithm]
We can talk of a
Self-Stabilizing System when the system, starting in any
condition, goes automatically through a series of transition
until it achieves an intended stable property. In the case of the
"leader" above, the system is self-stabilizing if, no matter
the initial state, after a finite time a "leader" is selected and
having a leader becomes a stable property of the system.
Stability and Self-Stabilization are fundamental properties when discussing
the reliability of distributed systems.
A distributed system is asynchronous if each node has its own clock and there are no fixed known deadlines on the delivery of messages. A distributed system is synchronous if we can assume a single clock for all the nodes and messages are delivered in a "unit of time" i.e. we can assume that when a new message is sent, all messages from the previous period have been delivered. A distributed system is semi-synchronous if there are known timeouts on the delivery of messages. This terminology on various aspects of time in the delivery of messages is extremely useful when discussing the properties of distributed systems and the assumptions we make on their operations.
Constants:
neighbors, the set of all the neighbors of the node.
Variables:
parent, initially nil, denotes the predecessor towards the
root of the current node
children, initially null, denotes the successors of the
current node in the rooted tree
other, initially null, denotes all the neighbors of
the current node that are not children of the
current node in the spanning tree.
When no message:
If self==r and parent == nil then
Set parent to r;
Send message "M" to all neighbors;
When receiving message "M" from neighbor pj:
If parent == nil then
Set parent to j;
Send message "Parent" to pj;
Send message "M" to all neighbors except pj;
else
Send message "Reject" to pj;
When receiving message "Parent" or "Reject" from neighbor pj:
if the message is "Parent" then
Add pj to children;
else
Add pj to other;
If all the neighbors are either in children or other or {parent} then
Terminate;
Notice that this algorithm is a kid of "flooding" algorithm and
involves a number of messages proportional to
e, the number of links in the distributed system.
Once the spanning tree is set up, communication involves many fewer
messages. For instance we can use it to broadcast
a message from the root to all other nodes, or, viceversa, to
convergecast a message from all the nodes to the root. Both
algorithms require a
number of messages proportional to the number of nodes
in the distributed system.
The Broadcast Algorithm is very simple: the root sends the message
to its children in the tree. Each child node sends
the message to its children.
The algorithm at each node terminates as soon as the transmission
to the children of the node has completed.
The Convergecast Algorithm is equally easy. Say that each node
keeps a value x and we want to send to the root the largest of these values.
Then the leaves send their value to their parent and terminate the algorithm.
Each not-leaf node, collects the message from each child plus its own
value, computes the maximum,
sends it to its parent, and terminates. The algorithm at the root
terminates as soon as all the messges from its children have been received.
Constants:
neighbors, the set of all the neighbors of the node.
Variables:
parent, initially nil, denotes the predecessor towards the
root of the current node
children, initially null, denotes the successors of the
current node in the rooted tree
leader, initially 0, denotes the best estimate at the
current node of who is the root of the tree.
unexplored, initially consists of all the neighbors of
the current node.
When no message:
If parent == nil then
Set parent to self;
Set leader to self;
Select and remove an element pk from unexplored;
Send message "leader"+leader to pk;
When receiving message "leader"+id from neighbor pj:
If leader < id then
Set leader to id;
Set parent to j;
Reset unexplored to consist of all neighbors except pj;
Reset children to null;
If unexplored != null then
Select and remove an element pk from unexplored;
Send message "leader"+leader to pk;
else
Send message "parent" to parent;
else if leader == id then
Send message "already" to pj;
When receiving message "parent" or "already" from neighbor pj:
If the message is "parent" then
Add j to children;
If unexplored != null then
Select and remove an element pk from unexplored;
Send Message "leader"+leader to pk;
else
If parent != self then
Send message "parent" to parent;
else
Terminate as root of spanning tree;
Notice that we said nothing about termination of the algorithms
anywhere but the root. The root can take care of that by broadcasting (now that
we have a spanning tree) a termination command before terminating itself.
The Dijkstra shortest path algorithm is run independently at each vertex after the vertex has collected all the information on the structure of the graph. A routing protocol distributes the needed information. The routing protocol associated with the Dijkstra shortest path algorithm (usually OSPF - Open Shortest Path First) allows each node to inform all other nodes of its own identity and of its links to its neighbors, its Link State. Link state information is exchanged periodically (every few seconds), or when a new neighbor comes on line, or when it is recognised that a link is disabled. The message traffic generated is limited, as long as the number of nodes in the network does not become too great [if we have n nodes and each node has E neighbors, the information transmitted is proportional to n*E]. The Dijkstra shortest path algorithm computes the routing tables fairly quickly, but it tends to use substantial memory resources and to be not too stable (i.e. routes may change substantially as a consequence of changes in the cost associated to a few links).
Initialize hashtables R and D so that for each vertex v of the
graph, R[v] = NIL, and D[v] is infinity except for s where D[s] = 0.
Finally let the set S consist of all the vertices of the graph.
Our intent is that for all vertices v, D[v] represents the current best
estimate of the cost of the paths from s to v and
R[v] is the next node (next-hop) in the current best path from
v to s.
While S is not empty
Let u be an element of S with minimal D value and remove it from S.
For each element v in the neighborhood of u that is in S
Let w = D[u] + cost-of-edge[u,v];
If D[v] is greater than w then //We are improving current path to v
Set D[v] to w;
Set R[v] to u;
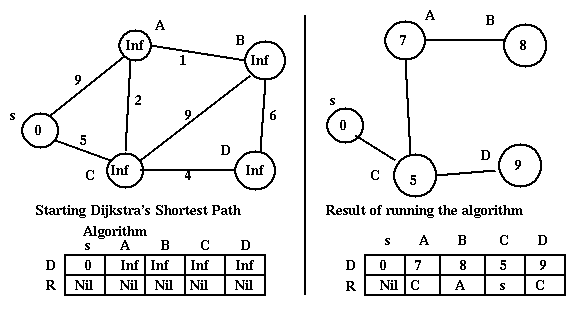
Note that Dijkstra's shortest path Algorithm creates a spanning tree with as root the node where the algorithm is run (s in the discussion above). The algorithm will result in different trees when run at different nodes - in fact each router node should run the algorithm). These spanning trees are not necessarily minimal (i.e. the sum of the cost of the branches is not minimal). For example:

However the tree built by the Dijkstra shortest path algorithm at s will give the paths of minimal length from s to each of the other nodes.