 CIS 307: Deadlocks
CIS 307: Deadlocks  CIS 307: Deadlocks
CIS 307: Deadlocks
Introduction
Deadlock occurs when we have a set of processes, each holding some
resources, each requesting some resources, and none of them is able to
obtain what it needs, i.e. to make progress. We will usually reason
in terms of resources R1, R2, .., Rm and processes P1, P2, .., Pn.
Resources can be preemptable or non-preemptable. A resource
is preemptable if it can be taken away from the process that is holding it
[we can think that the original holder waits, frozen, until the resource
is returned to it]. Memory is an example of a preemptable resource.
Of course, one may choose to deal with intrinsically preemptable resources
as if they were non-preemptable. In our discussion we only consider
non-preemptable resources.
Resources can be reusable or consumable. They are reusable
if they can be used again after a process is done using them. Memory, printers,
tape drives are examples of reusable resources. Consumable resources are
resources that can be used only once. For example a message or an event.
If two processes are waiting for a message and one receives it, then the
other process remains waiting. To reason about deadlocks when dealing
with consumable resources is extremely difficult. Thus we will restrict our
discussion to reusable resources.
Resources are usually with a multiplicity, i.e. an indication of how
many copies of the resource exist. So we may have 3 tape drives, 2 printers,
etc. We normally assume that resources have a multiplicity different than 1.
If it were always 1 the study of deadlocks could be simplified.
Resource Allocation Graphs
Resource Allocation Graphs (RAGs) are directed labeled
graphs used to represent,
from the point of view of deadlocks, the current state of a system.
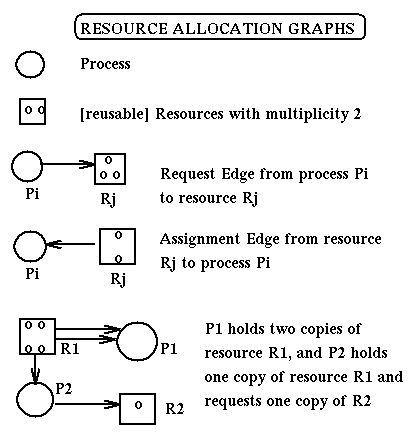
State transitions can be represented as transitions between the corresponding resource allocation graphs. Here are the rules for state transitions:
Here are some important propositions about deadlocks and resource allocation graphs:
Here is an example of reduction of a RAG:
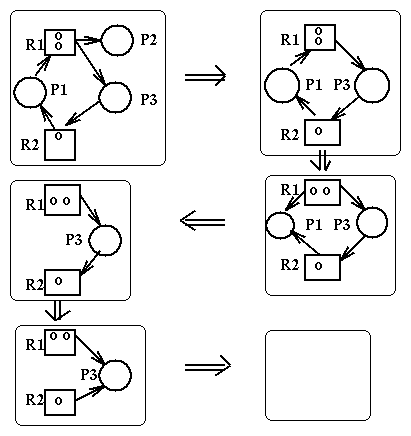
State Graphs
Where a resource allocation graph describes the current state of a system,
a State Graph describes from the point of view of deadlocks
all the states of a system.
Here is a system
P1:REPEAT P2:REPEAT
........ ........
1 request(Disk); 1 request(Tape);
........ ........
2 request(Tape); 2 request(Disk);
........ ........
3 release(Tape); 3 release(Disk);
........ ........
4 release(Disk) 4 release(Tape);
........ ........
FOREVER FOREVER
Here is the corresponding State Graph [the state of a program when
starting to execute a statement is the line number of that statement;
the state of a system is the ordered pair of the sates of the programs]:
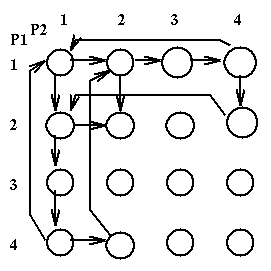
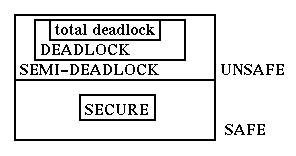
Here we see that state [2,2] is a deadlock state. If we had recognised also a state1.5 between statements 1 and 2 we would have created a more complex state graph where some states would be semi-deadlock states, i.e. states where the system is not yet deadlocked but it will have no choice but to become deadlocked. In general we can have the following kinds of states:
Deadlock Prevention
Deadlock Prevention is to use resources in such a way that we cannot
get into deadlocks. In real life we may decide that left turns are too
dangerous, so we only do right turns. It takes longer to get there but it
works. In terms of deadlocks, we may constrain our use of resources so that
we do not have to worry about deadlocks. Here we explore this idea with two
eaxmples.
It is easy to see that with this rule we will not get into deadlocks. [Proof by
contradiction.]
Here is an example of how we apply this rule. We are given a process that
uses resources ordered as A, B, C, D, E in the following manner:
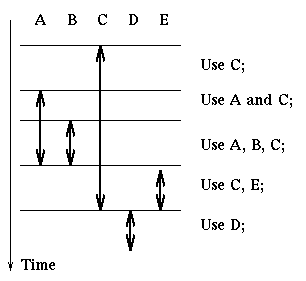
Then the process can do the following:
acquire(A); acquire(B); acquire(C);
use C
use A and C
use A, B, C
release(A); release(B); acquire(E);
use C and E
release(C); release(E); acquire(D);
use D
release(D);
A strategy such as this can be used when we have a few resources.
It is easy to apply and does not reduce the degree of concurrency too much.
Here is an example of use of this rule, locking a single resource at a time.
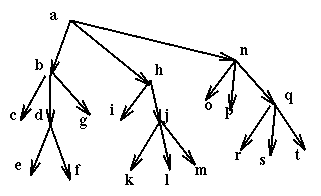
Then if a process wants to use the resources e, f, i, k it uses in sequence the commands:
Deadlock Avoidance and the Banker's Algorithm
Deadlock Avoidance, assuming that we are in a safe state
and we are requested certain resources, simulates the allocation of those
resources and determines if the resultant state is safe. If it is safe
the request is satisfied, otherwise it is delaied until it becomes safe.
The Banker's Algorithm is used to determine if a request can be satisfied. It uses the following variables:
procedure BANKER(REQUEST_I: array[1..m] of integer;
i : 1..n) is
{
if REQUEST_I > NEEDi then
ERROR; -- The user is asking more than the agreed maximum
repeat
while (REQUEST_i > AVAILABLE)
yield; -- Resources are not available at this time
ALLOCATION_i = ALLOCATION_i + REQUEST_i;
AVAILABLE = AVAILABLE - REQUEST_I;
if SAFE_STATE then
RETURN; -- The request is approved
ALLOCATION_i = ALLOCATION_I - REQUEST_i;
AVAILABLE = AVAILABLE + REQUEST_i;
YIELD; -- The request cannot safely be satisfied at this time
forever;
}
BOOLEAN function SAFESTATE is -- Determines if current state is safe
{ NOCHANGE : boolean;
WORK : array[1..m] of INTEGER = AVAILABLE;
FINISH : array[1..n] of boolean = [false, ..,false];
I : integer;
repeat
NOCHANGE = TRUE;
for I = 1 to N do
if ((not FINISH[i]) and
NEEDi <= WORK) then {
WORK = WORK + ALLOCATION_i;
FINISH[i] = true;
NOCHANGE = false;
}
until NOCHANGE;
return (FINISH == (true, .., true));
}
The time complexity of the Banker's algorithm as a function
of the number n of processes and m of resources is o(n*n*m).
Here is an example of use of the Banker's algorithm in the case of a single resource with multiplicity 12 and three processes, P1, P2, P3 which have a maximum need of, respectively, 10, 4, and 9. Currently these processes have respectively 5, 2, and 2 copies of the resource.
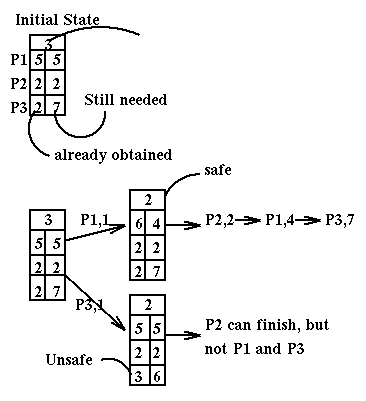
Note that we can use the SafeState routine to determine if we are in a deadlock state. More precisely, it recognizes unsafe states, i.e. deadlock and almost-deadlock states. But this is what we are usually interested in instead of just deadlock states.
In practice deadlocks are dealt with in a variety of ways. Prevention (linear ordering) for internal resources like PCBs and buffers; prevention (pre-emption by swapping out) for central memory; avoidance (banker's algorithm) for job resources like tape drives; pre-allocation with given maxima for swapping space; or just the Ostrich Solution (don't worry about the possibility of deadlocks) if they are sufficiently rare.
ingargiola.cis.temple.edu